"Mi desorden es atroz"
miércoles, 27 de marzo de 2019
martes, 26 de marzo de 2019
Pura vida
Iñaki Ochoa de Olza un luchador sin fin
Hoy me acordé de ti y quise compartir ese momento que tanto me acongojó, pero a la vez sentí una inmensa felicidad al saber que morías haciendo lo que más amabas y descansarías en esa inmensidad maravillosa.
Pura vida amigo mío
Hoy me acordé de ti y quise compartir ese momento que tanto me acongojó, pero a la vez sentí una inmensa felicidad al saber que morías haciendo lo que más amabas y descansarías en esa inmensidad maravillosa.
Pura vida amigo mío
domingo, 24 de marzo de 2019
La francesita
Algunas cosas desgraciadamente nunca cambian. El aprendizaje del ser humano sobre hechos que acontecieron en la historia no les enseñaron a cambiarlos, por muy dolorosos que estos fueran.
En memoria de aquellxs desaparecidx en democracia.
Las cunetas todavía sangran
La francesita » Ver-Pelis-Online | Películas Online Gratissábado, 23 de marzo de 2019
¿Qué son las estrellas de neutrones y quarks?
¿Qué son las estrellas de neutrones y quarks?
Antonio Claret
La evolución de una estrella está dictada por su masa y composición química iniciales. Cuanto más masiva es una estrella, más rápidamente agota sus fuentes de energía. Es como si cada estrella tuviera su propio DNI. Hoy día existen códigos numéricos informáticos que son capaces de reproducir la evolución estelar desde el colapso gravitacional inicial hasta las fases finales: enanas blancas, púlsares o agujeros negros, dependiendo de la masa inicial. Aquí nos centraremos en la evolución de las estrellas más masivas.
La evolución estelar se puede resumir en tres fases:
1) Pre-secuencia principal: La fuente de energía proviene del colapso gravitacional. Estas estrellas son relativamente frías y tienen un radio muy grande. Pueden pasar desde miles de años hasta millones de años en esta fase, dependiendo de la masa inicial. Son los llamados bebés estelares.
2) Secuencia principal: A medida que la estrella se va contrayendo, la temperatura en el núcleo aumenta, hasta que es lo suficientemente alta para la fusión del hidrógeno. La estrella pasará gran parte de su vida en la secuencia principal, dado que hay combustible suficiente para ello (de media, un 70% de la masa estelar está constituida de hidrógeno).
3) Fases finales: Una estrella masiva va progresivamente quemando hidrógeno, luego helio, carbono... formando elementos cada vez más pesados en su interior. Su estructura se parece a una cebolla y cada capa tiene una composición química distinta. Al llegar al hierro, no es posible sacar más energía de los procesos nucleares de fusión. El núcleo estelar de hierro restante debe soportar el peso de las capas superiores y se contrae formando un núcleo de neutrones. Las capas externas caen sobre este núcleo neutrónico y al tocarlo tiene lugar un rebote que envía este material al exterior con velocidades altísimas. ¡Tenemos una supernova! La energía asociada es enorme: del orden de 10**51 ergios. Gran parte de la energía de la explosión de una supernova se la llevan los neutrinos. ¡Solo el 1% de la energía está en el rango óptico!
El subproducto de una explosión de supernova en el rango de 8 y 20 masas producirá una estrella de neutrones.
Curiosidades de una estrella de neutrones
Radio: del orden de 10 km (depende de su masa)
Masa: del orden de la masa solar
Densidad en el centro: 10**15 g/cm3
Presión en el centro: 1**36 dyn/cm2
Campos magnéticos muy altos: Hay estrellas de neutrones aisladas y en sistemas binarios.
Observación: Pueden ser observadas en radio, en el visible, neutrinos, ondas gravitacionales, rayos x, gamma, etc.
La primera detección de exoplanetas confirmada se hizo en 1992, con el descubrimiento de varios planetas orbitando el púlsar PSR B1257+12.
El llamado púlsar Hulse-Taylor (PSR B1913+16) es un sistema de dos estrellas de neutrones donde por primera vez se detectaron, 'de forma indirecta', las ondas gravitacionales en 1974.
Estrellas de quarks
Por ahora, solo existen desde el punto de vista teórico. Son tambien llamadas “strange stars” (estrellas extrañas) y estan básicamente constituidas por quarks del tipo u, d y s.
Durante casi 40 años las estrellas de neutrones solo existieron en el papel pero, tras su descubrimiento en 1967, hoy día constituyen uno de los campos más avanzados de la astrofísica. Las estrellas de quarks, si son detectadas, puede que sigan una trayectoria similar, abriendo una ventana todavía más amplia a la física de los objetos compactos.
Antonio Claret es astrofísico teórico del Instituto de Astrofísica de Andalucía del CSIC en Granada.
https://www.muyinteresante.es/ciencia/articulo/que-son-las-estrellas-de-neutrones-y-de-quarks-361456152107
martes, 19 de marzo de 2019
viernes, 15 de marzo de 2019
Estamos vivos gracias a la energía oscura
La fuerza responsable de la expansión acelerada del Universo parece estar ajustada para permitir la formación de galaxias y, por ende, de la vida
MadridActualizado:
Si estamos vivos, es gracias a la energía oscura o, mejor dicho, gracias a su inexplicable debilidad. Esa es la conclusión de un impactante estudio recién publicado en arxiv.org en el que se recurre al principio antrópico (el mundo es necesariamente como es porque hay seres que se preguntan por qué es así) para justificar la intrigante debilidad de la fuerza que es responsable de la expansión acelerada del Universo.
Para Tomonori Totani, astrónomo de la Universidad de Tokio y autor principal del estudio, esta idea "crea un vínculo completamente nuevo entre energía oscura y astrobiología, campos que hasta ahora se habían considerados muy diferentes".
La mayoría de las personas no se ha parado a pensar que la energía oscura, la misteriosa fuerza que lo impregna todo y que obliga a las galaxias a separarse cada vez más unas de otras es, en realidad, particularmente débil. De hecho, si hacemos caso de la mecánica cuántica y de las ecuaciones de Einstein que describen la gravedad, la energía oscura debería ser, por lo menos, 120 ordenes de magnitud más fuerte de lo que es en realidad.
Sin embargo, si eso fuera así, ninguno de nosotros estaría aquí para observar el Universo y preguntarse, entre otras cosas, por la razón de la "debilidad" de la energía oscura. De hecho, si la energía oscura fuera tan poderosa como las teorías afirman que debería ser, habría separado mucho más deprisa la materia en el origen del Universo, impidiendo la formación de galaxias, estrellas y, por supuesto, de seres vivientes. Las leyes de la física, afirman muchos científicos invocando el principio antrópico, parecen estar ajustadas al milímetro para permitir la existencia de vida.
Totoni y sus colegas se preguntaron hasta qué punto una energía oscura más poderosa de la que observamos a nuestro alrededor podría seguir permitiendo la formación de galaxias y de seres vivos. Y por medio de una serie de simulaciones informáticas llegaron a la conclusión de que la materia podría seguir agrupándose para formar galaxias con una energía oscura que fuera entre 20 y 50 veces más fuerte de lo que es en realidad. Unos límites mucho más ajustados de los sugeridos por otros investigadores que sólo utilizaron las leyes de la física.
Galaxias tempranas
Los investigadores decidieron analizar con más detalle los modelos de Universo en los que la energía oscura era cerca de 50 veces más potente que en el nuestro. Y hallaron que, efectivamente, en esos universos aún podrían formarse galaxias, pero solo durante sus épocas más tempranas, antes de que el poder de la misteriosa energía oscura prevaleciera y terminara por alejar todo de todo.
Dado que, además, un Universo primitivo es mucho más denso que otro de larga vida, en el que la materia está ya muy separada, las galaxias que lograran formarse estarían llenas de estrellas que se apiñarían hasta 10 veces más de lo que lo hacen en nuestra Vía Láctea.
En esas galaxias tan densas, todas las estrellas estarían realmente muy cerca de sus vecinas. Y las estrellas muy masivas, que suelen vivir vidas muy cortas y explotar después como supernovas, liberarían dosis letales de radiación a los sistemas estelares cercanos y a sus planetas, esterilizándolos y haciendo imposible que la vida se desarrolle en ellos.
Los investigadores calcularon que este efecto, que previamente nunca había sido considerado, convertiría los Universos con una energía oscura muy fuerte en inhóspitos para la vida.
Por lo tanto, la "debilidad" de la energía oscura es, precisamente, la razón por la que estamos aquí. Según Totani, su propuesta podría cobrar fuerza si en el futuro, los astrobiólogos encuentran que la vida es mucho más rara en las regiones más densas de la galaxia.
jueves, 14 de marzo de 2019
El amor y el odio de Einstein por la física cuántica
El amor y odio de Einstein por la física cuántica
Si existe un científico que casi cualquier persona de la calle sabría nombrar, ése es sin duda Albert Einstein. Como relataba Jürgen Neffe en su biografía, Einstein fue el primer científico mediático de la historia, ascendido a la categoría de ídolo cuando el diario londinense The Timesdivulgó en 1919 que la teoría de la relatividad general había quedado demostrada gracias a las fotografías de un eclipse de sol que revelaban la curvatura de la luz de las estrellas, como el físico había predicho.
Einstein recibió el Nobel de Física en 1921. Pero aunque su nombre ha quedado míticamente ligado a su teoría de la relatividad y su famosa ecuación E=mc2, no fue este logro el que le hizo merecedor del premio, sino su explicación del efecto fotoeléctrico, un fenómeno que Heinrich Hertz había observado en 1887. En 1905, Einstein describió cómo la luz arrancaba del metal paquetes discretos de energía, llamados cuantos. La idea de los cuantos de luz fue el germen de una revolución científica, que en las primeras décadas del siglo XX daría lugar al desarrollo de la física cuántica.
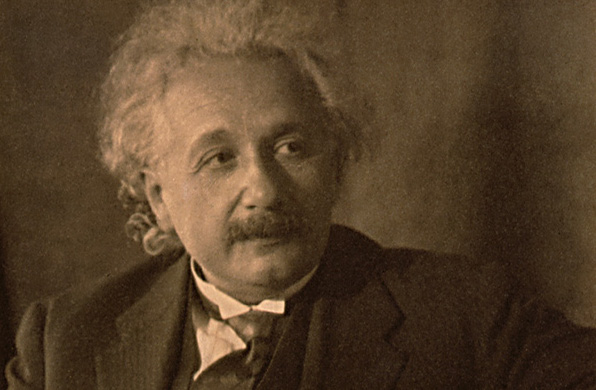Albert Einstein en un retrato de 1931. Crédito: Biblioteca del Congreso de EE. UU.
A pesar de haber abierto el camino hacia una nueva física, Einstein mantuvo una extraña relación de recelo hacia la visión sostenida por quienes lideraban este vibrante campo de la ciencia. Físicos como Heisenberg o Schrödinger introdujeron con total naturalidad conceptos que se alejaban del realismo, como que la acción del observador determinaba las propiedades del sistema, o que un átomo podía estar intacto y desintegrado al mismo tiempo (o un gato vivo y muerto a la vez, en el ejemplo metafórico más famoso de Schrödinger).
“DIOS NO JUEGA A LOS DADOS”
Pero para Einstein, esta dependencia de la probabilidad sugería más bien un desconocimiento de las leyes implicadas en el gobierno de la realidad. “Estoy convencido de que Él [Dios] no juega a los dados”, escribió en una carta al también físico Max Born. En otra ocasión le preguntó a su biógrafo Abraham Pais si creía que la luna sólo existía cuando la miraban.
En 1935 Einstein publicó, junto a sus colegas Boris Podolsky y Nathan Rosen, un experimento mental que hoy conocemos como la paradoja EPR. Existe la posibilidad de que dos partículas compartan sus propiedades, como si fueran gemelas. Pero si, como defendía la corriente mayoritaria de la cuántica, la acción de un observador sobre una de ellas debía influir en la otra, esto implicaría que existía una comunicación instantánea entre ambas. Lo cual, argumentaban Einstein y sus colaboradores, rompía el irrompible límite de la velocidad de la luz. Debían existir por tanto “variables ocultas” según las cuales el sistema obedecía a una especie de programación previa.
Titular sobre Einstein y la teoría cuántica del New York Times en 1935. Crédito: New York Times
En conclusión, la física cuántica no estaba equivocada, pensaba Einstein; simplemente estaba incompleta. Del mismo modo que la relatividad general había descrito un tejido del espacio-tiempo que ligaba los cuerpos entre sí, eliminando la necesidad de una acción gravitatoria a distancia que había desconcertado al propio Isaac Newton, Einstein creía que estas variables ocultas en el entorno local de las partículas antes de su separación explicarían su comportamiento posterior sin recurrir a lo que llamaba una “truculenta acción a distancia”.
UNA DISCUSIÓN DE DÉCADAS
La paradoja EPR alimentó vivas discusiones entre los físicos durante décadas, pero fue en 1964 cuando el norirlandés John Stewart Bell descartó la existencia de variables ocultas que pudieran explicar lo que hoy conocemos como entrelazamiento cuántico. Como consecuencia del teorema de Bell, se concluía que sí existía una acción a distancia no local entre las partículas.
Conceptualización artística sobre el entrelazamiento cuántico. Crédito: YouTube/Stargazer
Sin embargo, el enunciado de Bell no zanjó el debate. En años posteriores, otros físicos han emprendido el empeño de tapar las posibles grietas (o loopholes) de los experimentos de entrelazamiento cuántico que podrían abrir una vía a otras explicaciones dentro de la visión realista einsteniana. Por ejemplo, los críticos arguyen que los experimentos pueden estar viciados por errores de los aparatos o por sesgos de los investigadores.
Entre los físicos que han tratado de blindar los experimentos de entrelazamiento cuántico contra cualquier posible fisura se encuentra Ronald Hanson, de la Universidad de Tecnología de Delft (Holanda). “Los experimentos libres de loopholes de 2015, de los cuales el nuestro fue el primero, han cerrado todos los loopholes que pueden cerrarse”, afirma Hanson a OpenMind. “¿Prueba esto la existencia del entrelazamiento? Yo mejor lo diría al revés: la visión de causalidad local, o de realismo local, se ha demostrado falsa”, afirma Hanson.
A FAVOR DEL ENTRELAZAMIENTO CUÁNTICO
Pero aún hay quienes sostienen que el escaso tiempo transcurrido entre la generación de las partículas y su medición en los experimentos de entrelazamiento podría seguir avalando la idea de la programación. Un reciente experimento ha tratado de derribar esta posible fisura midiendo fotones procedentes de estrellas de hasta 600 años luz de distancia; es altamente improbable, sostienen los investigadores, pensar en una programación de las partículas capaz de durar 600 años. No obstante, para Hanson estos llamados experimentos “cósmicos” de Bell no aportan un avance fundamental, ya que no descartan la influencia de variables ocultas.
Según David Kaiser, físico del Instituto Tecnológico de Massachusetts y coautor de este último estudio, “aún es un poco pronto para proclamar que el entrelazamiento cuántico ha sido definitivamente probado”. El motivo, expone Kaiser, es que los últimos experimentos realizados hasta ahora han tapado fisuras de dos en dos, pero no tres al mismo tiempo. “Pero el progreso reciente en este campo parece más sugerente que nunca en favor del entrelazamiento cuántico”.
¿Significa esto que el gran Einstein finalmente falló al recelar de la cuántica? Si los experimentos actuales le habrían hecho cambiar de opinión o no, “¡quién puede decirlo!”, concluye Kaiser. Por su parte, Hanson aporta un matiz: “Mi visión es que Einstein fue uno de los primeros en descubrir las consecuencias no locales de la teoría cuántica”, pero “no creyó que esas consecuencias pudieran ser ciertas”. Si hubiera tenido la oportunidad de presenciar los avances más recientes, prosigue Hanson, “lo habría aceptado como hechos de la naturaleza; ¡era un hombre muy listo!”.
Javier Yanes para Ventana al Conocimiento
@yanes68
Revelan lo comunes que eran los agujeros negros supermasivos en el universo temprano
Revelan lo comunes que eran los agujeros negros supermasivos en el universo temprano.
2019-03-14 | Dra Amelia Ortiz
Luz de uno de los cuásares más lejanos conocidos, alimentado por un agujero negro supermasivo que se halla a 13050 millones de años-luz de la Tierra. Los demás objetos del campo son principalmente estrellas de nuestra Vía Láctea y galaxias a lo largo de la línea visual. Crédito: NAOJ.
Un equipo de astrónomos ha descubierto en el universo lejano 83 cuásares alimentados por agujeros negros supermasivos, en una época en la que el Universo tenía menos del 10 por ciento de su edad actual. El hallazgo incrementa considerablemente el número de agujeros negros conocidos en esa época y revela, por primera vez, lo comunes que eran al principio de la historia del Universo.
Los agujeros negros supermasivos se encuentran en los centros de las galaxias y poseen masas equivalentes a millones e incluso miles de millones de veces la del Sol. Aunque son predominantes en el Universo actual, no está claro cuándo se formaron y cuántos de ellos existen en el Universo temprano lejano. Aunque los agujeros negros supermasivos distantes son identificados como cuásares que brillan cuando engullen gas, los estudios anteriores eran sensibles solo a los cuásares más luminosos y raros y, por tanto, a los agujeros negros más masivos. Los nuevos descubrimientos muestran la población que posee masas características de los agujeros negros más comunes observados en el Universo actual y, por tanto, arrojan luz sobre su origen.
Además esta investigación aporta datos nuevos acerca del efecto de los agujeros negros sobre el estado físico del gas presente en el Universo temprano en sus primeros mil millones de años. Se acepta que el hidrógeno del Universo era neutro en el pasado pero que fue “reionizado” (es decir, separado en sus protones y electrones componentes) en la época en que nació la primera generación de estrellas, galaxias y agujeros negros supermasivos, en los primeros cientos de millones de años después del Big Bang.
Una hipótesis sugiere que hubo muchos más cuásares en el Universo temprano de lo detectado anteriormente y que fue la suma de su radiación lo que reionizó el Universo. Sin embargo, la densidad en número medida en esta investigación es significativamente menor de lo que se necesita para explicar la reionización. Por tanto, la reionización fue causada por otra fuente de energía, con mayor probabilidad por las numerosas galaxias que empezaron a formarse en el Universo joven.
Fuente: SUBARU.
martes, 12 de marzo de 2019
El campo magnético de Júpiter puede estar agitando el océano de Europa
El campo magnético de Júpiter puede estar agitando el océano de Europa
12 de marzo de 2019NASA / JET PROPULSION LAB-CALTECH / SETI INSTITUTE
MADRID, 12 Mar. (EUROPA PRESS)
El campo magnético de Júpiter podría estar causando una corriente de chorro en el océano subterráneo de Europa, según evidencias obtenidas de los datos de la nave espacial Galileo.
En su artículo publicado en la revista Nature Astronomy, Christophe Gissinger, de la École Normale Supérieure, y Ludovic Petitdemange, del Laboratory for Studies of Radiation and Matter in Astrophysics and Atmospheres, comenzaron señalando que Júpiter tiene un campo magnético muy fuerte, lo suficientemente fuerte como para alcanzar e impactar sus lunas.
También que el océano subterráneo de Europa es salado. Un campo magnético que influye en un mar salado resultaría en la conducción de electricidad, lo que probablemente creará una corriente de chorro en el océano.
Para descubrir qué tipo de movimiento podría ocurrir y para descubrir otros posibles impactos del campo magnético en el océano lunar, los investigadores crearon simulaciones numéricas.
Las simulaciones mostraron una corriente en chorro que se formaba en algún lugar cerca del ecuador de la luna, moviéndose tan rápido como unos pocos centímetros por segundo y fluyendo en sentido opuesto al giro de la luna. Tal flujo opuesto, señalaron los investigadores, daría lugar a un estrés en la superficie de la luna, que ocasionalmente podría formar grietas.Esto explicaría las grietas superficiales observadas en Europa por otros investigadores.
Además, señalan que no toda la energía del campo magnético se transferiría al océano; parte de ella se disiparía de la luna, probablemente alrededor de los polos. Y si ese fuera el caso, habría evidencia de que la capa de hielo de la luna se estaba adelgazando a medida que el agua derritiéndose llegaba a la superficie. Y nuevamente, eso es justo lo que se ha observado: penachos de agua que brotan de lugares cercanos a los polos.
Los investigadores sugieren que una corriente de chorro en Europa podría compararse con la Corriente del Golfo aquí en la Tierra. En particular, la corriente en chorro terrestre mueve compuestos alrededor del océano que son importantes para la vida. Si Europa alberga vida, su corriente en chorro podría tener el mismo propósito.
lunes, 11 de marzo de 2019
domingo, 10 de marzo de 2019
Extraordinarios anillos del sistema solar
Elaborado por Materia para OpenMind
08 marzo 2019
Los extraordinarios anillos del sistema solar
Al igual que los olímpicos, son cinco los sistemas de anillos planetarios que conocemos hasta el momento en nuestro sistema solar. Los de Saturno son los más visibles y llamativos, pero ya no son los únicos, tras la cadena de descubrimientos de las últimas cuatro décadas. El 10 de marzo de 1977 detectamos los de Urano, que con 13 anillos es el planeta que más posee. Dos años más tarde, en 1979, pudimos divisar los que rodean al gigante gaseoso Júpiter. Después encontramos los del azul Neptuno, en 1989; y ya en 2013, supimos que el planetoide Chariklo, entre Saturno y Urano, presentaba un anillo doble. ¿Esconderá más aros nuestro sistema solar?
LAS “ASAS” DE SATURNO QUE VIO GALILEO
El primero en ver los anillos de Saturno fue Galileo Galilei en 1610. Para su sorpresa, aquella estrella errante mostraba una especie de “asas o brazos”, que no logró ver con claridad debido a sus rudimentarios telescopios. Casi 50 años más tarde, el holandés Christiaan Huygenscomprobó que aquellas “asas” de Saturno eran un anillo. Desde entonces, se sucedieron las descripciones de aquel misterioso aro, aunque nadie sabía de qué estaban compuestos.
LOS TRECE ANILLOS DE URANO
LOS AROS ROJIZOS DEL GIGANTE JÚPITER
LIBERTAD, IGUALDAD Y FRATERNIDAD EN NEPTUNO
LA DOBLE SORPRESA DEL PLANETOIDE CHARIKLO
Bibiana García Visos
La velocidad fimita de la luz. Cultura científica
La velocidad finita de la luz
Ío con Júpiter de fondo. Fuente: NASA
Dado que podemos considerar quela luz viaja en línea recta, ¿podemos decir a qué velocidad lo hace? Galileo abordó este problema en sus Discorsi e Dimostrazioni Matematiche Intorno a Due Nuove Scienze, publicado en 1638. Señaló que las experiencias cotidianas podrían llevarnos a concluir que la luz se propaga instantáneamente. Pero que estas experiencias, cuando se analizan más de cerca, solo muestran que la luz viaja mucho más rápido que el sonido. Por ejemplo, “cuando vemos disparar una pieza de artillería a gran distancia el destello llega a nuestros ojos sin que transcurra tiempo; pero el sonido llega al oído solo después de un intervalo perceptible”.
Pero, ¿cómo sabemos realmente si la luz se movió “sin que transcurra tiempo” a menos que tengamos alguna forma precisa de medir el lapso de tiempo? Galileo continúa describiendo un experimento mediante el cual dos personas que se encontrasen en colinas distantes y usando linternas podrían medir la velocidad de la luz. Concluyó que la velocidad de la luz era probablemente finita, no infinita. Galileo, sin embargo, no estima un valor definido concreto.
Las pruebas experimentales se relacionaron con éxito por primera vez con una velocidad finita para la luz por un astrónomo danés, Ole Rømer. Las observaciones detalladas de los satélites de Júpiter habían mostrado una irregularidad inexplicable en los tiempos registrados entre los eclipses sucesivos de los satélites por el planeta. Se esperaba que un eclipse del satélite Ío ocurriera exactamente 45 s después de las 5:25 de la mañana del 9 de noviembre de 1676 (calendario juliano). En septiembre de ese año, Rømer anunció a la Academia de Ciencias de París que el eclipse observado llegaría 10 minutos tarde. El 9 de noviembre, los astrónomos del Observatorio Real de París estudiaron cuidadosamente el eclipse. Aunque escépticos, informaron que el eclipse ocurrió tarde, tal como lo había previsto Rømer.
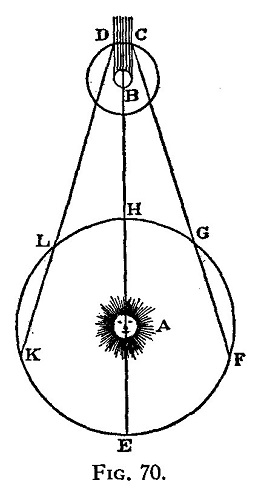
Ilustración empleada por Rømer en su informe Demonstration tovchant le mouvement de la lumiere trouvé par M. Römer de l’ Academie Royale des Sciences, fechado el 7 de diciembre de 1676. A: Sol; B: Júpiter; DC: Ío
Más tarde, Rømer reveló la base teórica de su predicción a los desconcertados astrónomos en la Academia de Ciencias. Explicó que el tiempo originalmente esperado del eclipse se había calculado a partir de observaciones hechas cuando Júpiter estaba cerca de la Tierra. Pero ahora Júpiter se estaba más lejos. El retraso en el eclipse ocurrió simplemente porque la luz procedente de las inmediaciones de Júpiter, donde ocurría el eclipse, necesita un tiempo para llegar a la Tierra. Obviamente, este intervalo de tiempo debe ser mayor cuando la distancia relativa entre Júpiter y la Tierra en sus órbitas es mayor. De hecho, Rømer estimaba que la luz necesita alrededor de 22 minutos para cruzar la propia órbita de la Tierra alrededor del Sol.
Poco después, el físico holandés Christian Huygens utilizó los datos de Rømer para realizar el primer cálculo de la velocidad de la luz. Huygens combinó el valor de Rømer de 22 minutos para que la luz cruzara la órbita de la Tierra con su propia estimación del diámetro de la órbita de la Tierra. Huygens obtuvo un valor para la velocidad de la luz en el espacio que, en unidades modernas, es de aproximadamente 200.000 km/s. Esto es, aproximadamente dos tercios del valor actualmente aceptado. El error en el valor de Huygens se debió principalmente a que Rømer sobrestimó el intervalo de tiempo. Ahora sabemos que la luz solo necesita unos 16 minutos para cruzar la órbita de la Tierra.
La velocidad de la luz se ha medido de muchas maneras diferentes desde el siglo XVII. El desarrollo de dispositivos electrónicos en el siglo XX permitió mediciones muy precisas, haciendo de la velocidad de la luz una de las constantes físicas medidas con mayor precisión. Debido a la importancia del valor de la velocidad de la luz en las teorías físicas modernas*, en la actualidad su valor no se mide, sino que está definido a consecuencia de la definición de metro y es, exactamente, de 299,792,458 metros por segundo.La velocidad de la luz suele estar representada por el símbolo c.
sábado, 9 de marzo de 2019
miércoles, 6 de marzo de 2019
Inga Hjalmars
Inga Fischer-Hjalmars: de la farmacia a la mecánica cuántica para convertirse en la pionera sueca de la química teórica
La vida científica de Inga Fischer-Hjalmars estuvo siempre guiada por una curiosidad insaciable pero comenzó condicionada por un detalle mucho más mundano: hija de una familia sin muchos recursos económicos, buscó los estudios científicos más cortos posibles para empezar a trabajar cuanto antes.
Así, nacida el 16 de enero de 1918 en Estocolmo, en 1939 obtenía su título en Farmacia, que por entonces duraba dos años. De ahí no tardaría en pasar a otras especialidades que conforman una carrera verdaderamente multidisciplinar. Le espoleaban las ganas de “saber lo que pasa realmente dentro de una molécula” y acceder así al conocimiento más básico sobre la materia y la naturaleza.
De la Farmacia a la química teórica
Como decimos, pronto la farmacia y la bioquímica se le quedaron cortas: en 1944 obtuvo un máster en matemáticas, química y física, en 1949 otro título en mecánica y un año después en química. La combinación de sus conocimientos de farmacia y química la llevaron a participar en el descubrimiento de la xilocaína, un analgésico local también conocido como lidocaína.
Durante este periodo, durante un año y medio, trabajó como asistente de Ulf von Euler, médico y farmacéutico ganador del Nobel en Fisiología o Medicina en 1907 por su trabajo sobre los intercambios químicos en las terminaciones nerviosas.
En aquella época no se podían obtener becas o fondos solo por estudiar, así que todo el que no tenía padres ricos tenía que ganar dinero.
Inga Fischer-Hjalmars en [1]
Lars Ehrenberg, Gunnar Widmark, Bengt Lundquist, Inga Fischer, Gunnar Molander, y Elis Sundström.
Fotografía: Astra-Zeneca. Extraída de [4].
En 1947, en colaboración con Charles Coulson, reputado químico teórico de la Universidad de Oxford, publicó un artículosobre cómo describir la disociación de un enlace químico, que fue de gran repercusión para el avance de este campo científico.
“Si una mujer puede, por qué no las demás”
Con la intención de conocer a fondo el comportamiento de estas moléculas comenzó a estudiar física teórica, y terminó doctorándose en la Universidad de Estocolmo en 1952. En 1963 sustituyó a su director de tesis, Oskar Klein, como profesor de física teórica de la universidad, convirtiéndose así en la primera mujer en ocupar este puesto en Suecia. Con el tiempo, fue teniendo cada vez más alumnas:
Parece que se dieron cuenta de que si una mujer podía hacerlo, por qué no las demás.
Inga Fischer-Hjalmars en [1]
Fischer-Hjalmars fue una de los dos pioneros de la química teórica en ese país. El profesor Per-Olov Löwdin, que era el otro, estaba más orientado a las matemáticas y la física, mientras que ella, debido a su formación previa en farmacia, dirigió sus esfuerzos a métodos que pudiesen emplearse en química orgánica y en bioquímica.
En general, dedicó gran parte de su carrera a utilizar la mecánica cuánticapara responder cuestiones y problemas de la química teórica, desvelando así los secretos del comportamiento básico de las moléculas que conforman la materia. De hecho, el desarrollo de la química teórica en su país se debe en gran parte a su labor científica, ya que era una disciplina que apenas comenzaba a despuntar cuando ella inició su carrera.
Reconocimiento y activismo… pero no un Nobel
Imagen extraída de [4].
Su trabajo fue reconocido a nivel nacional y en 1978 pasó a formar parte de la Real Academia de las Ciencias de Suecia, así como de la Real Academia Danesa de Ciencias y Letras. También obtuvo reconocimiento internacional al pasar a formar parte de la International Academy of Quantum Molecular Science.
Además, Inga Fischer-Hjalmars desarrolló una intensa vida activista defendiendo las causas en las que creía. Fue entre otras cosas presidenta del Comité Permanente del Consejo Internacional de Uniones Científicas sobre Libre Circulación de Científicos, una organización que defendía el libre trabajo y movimiento de los científicos disidentes y judíos que vivían dentro de la Unión Soviética y que vieron gravemente limitada o impedida su tarea bajo ese régimen. Por esta labor fue recompensada con el Premio de los Derechos Humanos de los Científicos, concedido por la Academia de Ciencias de Nueva York.
Fischer-Hjalmars falleció en 2008. A pesar de sus avances en campos tan complejos y tan inexplorados, y de haber nacido y trabajado en Suecia, la cuna del Nobel, nunca ganó uno, pero eso no pareció importarle demasiado:
Nunca pensé en ello. Me di cuenta de que no trabajaba en un área que encajase en ninguna categoría de los Nobel. Y tampoco me parecía tan interesante, interesante es poder dar algunos pequeños pasos que hagan avanzar las cosas.
martes, 5 de marzo de 2019
Los hechos en mecánica cuántica dependen del observador
La ciencia de la mula Francis
Los «hechos» en mecánica cuántica dependen del observador
El resultado de una medida de un sistema cuántico se puede considerar un «hecho» observado. ¿Son estos «hechos» independientes del observador? No, en mecánica cuántica todo «hecho» depende del observador. Caslav Brukner (Univ. Viena, Austria) demostró un teorema no-go que así lo afirma y propuso un experimento de tipo Bell inspirado en el amigo de Wigner para comprobarlo. Alessandro Fedrizzi (Univ. Heriot-Watt, Edimburgo, Reino Unido) y sus colegas han realizado este experimento con fotones, que toman el papel de los dos superobservadores (los dos Wigner) y de los dos observadores (los dos amigos de Wigner). Así se ha verificado de forma experimental el teorema de Brukner (como no podía ser de otra forma si suponemos que la mecánica cuántica describe nuestro universo). Como hubiera dicho Einstein, si el experimento hubiera contradicho el teorema, no hubiera fallado el teorema, sino el experimento.
Por supuesto, como todos los experimentos de tipo Bell, no está libre de todas las posibles lagunas (o resquicios). La desigualdad CHSH (por Clauser–Horne–Shimony–Holt) afirma que la probabilidad conjunta de los resultados de las cuatro medidas (dos de los observadores y dos de los superobservadores) debe ser menor que 2 (si existe una teoría clásica local subyacente descrita mediante variables ocultas que explica el resultado). Las medidas experimentales (tras estudiar las 64 configuraciones posibles en 1794 repeticiones tras 360 horas de trabajo) ofrecen un valor de 2.416 ± 0.075, una violación de la desigualdad CHSH a más de cinco sigmas (desviaciones estándar). Un resultado rotundo donde los haya (aunque siempre en Física habrá que esperar a que sea repetido de forma independiente). Los «hechos» (resultados de las medidas cuánticas) son dependientes del observador.
El artículo es Massimiliano Proietti, Alexander Pickston, …, Alessandro Fedrizzi, “Experimental rejection of observer-independence in the quantum world,” arXiv:1902.05080 [quant-ph]; el teorema no-go y el experimento mental es publicó en Caslav Brukner, “A no-go theorem for observer-independent facts,” Entropy 20: 350 (2018), doi: 10.3390/e20050350, arXiv:1804.00749 [quant-ph]. En la tertulia del podcast Coffee Break: Señal y Ruido se habló de este tema (LCMF, 01 Mar 2019) al hilo de los «hechos alternativos» en el titular de la pieza de Anil Ananthaswamy, “Quantum experiment suggests there really are ‘alternative facts’,” New Scientist, 22 Feb 2019.
La presentación detallada de un experimento de tipo Bell requiere usar matemáticas. Sin ellas, los razonamientos parecen pura «magia cuántica». Debo empezar recomendando la lectura del libro de John S. Bell, “Lo decible y lo indecible en mecánica cuántica”, Alianza Editorial (1991). Solo tras acostumbrarse a los experimentos de tipo Bell más sencillos se pueden entender los más refinados publicados muchasdécadas más tarde. Como dice la reseña de Carlos Sabín Lestayo, “Confusión cuántica. Tópicos peligrosos en la divulgación de la física cuántica”, Investigación y Ciencia (Feb 2019) [reseña gratuita], mucha gente afirma que no se entiende la mecánica cuántica al hilo de la célebre boutade de Richard Feynman: «Creo que puedo decir con seguridad que nadie entiende la mecánica cuántica». “Las malas citas, sacadas de contexto y sin conocer la fuente original, son una de las plagas de nuestros tiempos. [Siendo] cierto que Feynman pronunció esas palabras, ¿seguro que quería decir lo que parece que quería decir? Si saben inglés, pongan «Richard Feynman, why» en YouTube y prepárense a disfrutar durante siete minutos”.
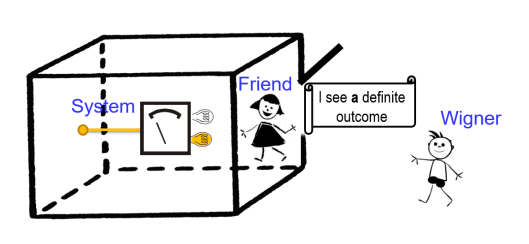
En el experimento del amigo de Wigner intervienen un superobservador(Wigner), capaz de realizar medidas cuánticas sobre sistemas macroscópicos (todo el laboratorio que contiene a su amigo y un cúbit) y un observador (el amigo de Wigner) que solo es capaz de realizar medidas cuánticas sobre sistemas microscópicos. Wigner lo ignora, pero su amigo ha realizado una medida cuántica sobre el cúbit, ha anotado que lo ha hecho en una carta sin indicar el resultado y se la ha enviado por correo a Wigner. Wigner para conocer el estado del cúbit aplica una operación cuántica al laboratorio que borra el estado de la memoria de su amigo y realiza una medida del estado conjunto. Antes de leer la nota, Wigner usa el resultado de su medida para inferir el valor del cúbit. Sin embargo, un día después, tras leer la nota, descubre que su cálculo está mal y que si su amigo ha realizado la medida, su predicción original está en contradicción con lo que ha podido medir el amigo. ¿La mecánica cuántica es incoherente? No, todo lo contrario, tras conocer la nota Wigner debe reevaluar el resultado de su experimento. Si lo hace siguiendo las leyes de la mecánica cuántica, su resultado será compatible con la observación del amigo.
Sean Wigner y su amiga (sigo el dibujo de Brukner); sea el sistema cuántico medido un espín (
Siendo un superobservador, Wigner puede realizar una medida tipo Bell de este sistema macroscópico en la base
y
La medida arrojará un resultado que permitirá a Wigner predecir en qué estado está el espín. Pero Wigner no sabe que su amiga le ha enviado una carta; cuando la recibe se da cuenta de que el estado del sistema macroscópico es
Ahora se da cuenta de que su inferencia anterior del estado del espín a partir del resultado de su medida es incorrecta. Como experto en mecánica cuántica, revisará sus cálculos. Los «hechos» para Wigner (resultados de sus medidas) y los «hechos» para su amiga (resultados de las de ella) han coexistido (hasta que Wigner recibió la carta) como «hechos» dependientes del observador. Solo tras la recepción de la carta y la reevaluación del significado de los resultados sobre el estado del espín estos «hechos» se consensúan y adquieren la propiedad de ser «hechos» sobre el espín independientes del observador.
Este experimento se puede complicar si contamos con dos Wigner (superobservadores) y dos amigos de Wigner (observadores). Y más aún, si tenemos en cuenta el orden temporal en el que se realizan las medidas cuánticas. Así llegamos a un experimento engorroso de analizar en el que es muy fácil perder el hilo y acabar realizando operaciones matemáticas en contra de los postulados de la mecánica cuántica. Por ejemplo, suponer que la evolución es unitaria tras una medida, como si no hubiera ocurrido una proyección del estado (el mal llamado colapso). Ya te puse un buen ejemplo en “El error del artículo de Frauchiger y Renner sobre la inconsistencia de la mecánica cuántica”, LCMF, 29 Oct 2018; en rigor tendría que haber titulado «incoherencia», evitando el anglicismo «inconsistencia», un falso amigo bien conocido). Si todas las medidas son unitarias (ninguna tiene proyección el estado), o si todas las medidas incluyen una proyección del estado (ninguna es unitaria), el resultado siempre está de acuerdo con la mecánica cuántica y no hay ningún tipo de incoherencia. Pero si seguimos los cálculos realizados por Frauchiger y Renner al pie de la letra, con medidas que a veces proyectan el estado y que otras veces no lo proyectan, aparece una incoherencia. Pero su origen no es la incoherencia de la mecánica cuántica, como ellos afirman y los medios cacarean, sino la incoherencia del análisis realizado por Frauchiger y Renner.
El teorema no-go de Brukner afirma que no existen hechos independientes del observador. En concreto, se demuestra que las cuatro afirmaciones siguientes son contradictorias: (1) la teoría cuántica es válida (en nuestro universo y a todas las escalas); (2) las medidas cuánticas de los observadores son locales (no se propaga información entre observadores más rápido que la velocidad de la luz en el vacío); (3) el universo no es superdeterminista (los observadores tienen libre albedrío a la hora de preparar el estado de sus sistemas de medida); y (4) los «hechos» (resultados de las medidas registrados en memorias físicas) son independientes del observador. Como todo físico que acepta la mecánica cuántica considera que las tres primeras afirmaciones son incuestionables, la conclusión es que todos los «hechos» son dependientes del observador.
Para confirmar su teorema de forma experimental, Brukner nos propone el experimento ilustrado en esta figura, con dos Wigner (superobservadores) llamados Alicia y Berto, y dos amigos (observadores) llamados Carlos y Débora. Entre los dos laboratorios hay generador de una pareja de espines entrelazados que se envían hacia Carlos, sea 
donde
y
En ángulo 
Carlos y Débora realizarán una medida de sus respectivos espines a lo largo del eje
donde
Se definen los resultados observados para los espines en los ejes 
y
y los análogos 
La desigualdad de tipo Bell para este experimento será de tipo Clauser-Horne-Shimony-Holt (CHSH). Por tanto, relacionará la probabilidad conjunta 
y de forma similar en los otros casos, donde se han tomado valores numéricos para 
El cálculo cuántico, es decir, que usa amplitudes de probabilidad en lugar de probabilidades, conduce a una cota superior diferente 
Esta figura muestra el esquema experimental de la implementación óptica de Proietti y sus colegas del experimento mental de Brukner. En lugar de humanos se usan fotones como observadores y superobservadores, y también en lugar de los dos espines. En rigor la mecánica cuántica permite que el observador sea una sistema cuántico; lo único que caracteriza al observador es disponer de una memoria en la que se almacene el resultado de la medida (es decir, la capacidad de generar un «hecho»; los filósofos que lean esto sabrán que hay otras definiciones del término «hecho», pero nos alejaría de nuestro objetivo discutirlas). Gracias a ello se puede implementar un superobservador capaz de observar un observador, es decir, un sistema cuántico capaz de medir a un sistema cuántico capaz de medir a un sistema cuántico. En algunos foros de la web se ha criticado que en este experimento todos los sistemas cuánticos sean fotones; se sugiere que una implementación más rigurosa exige que el sistema observado, los observadores y los superobservadores sean sistemas físicos diferentes. En rigor es innecesario, lo que no quitará que un futuro muy cercano se logre dicha implementación. Usando solo fotones todas las operaciones cuánticas se realizan con tecnología fotónica en una mesa óptica, lo que facilita la implementación del experimento, que no es sencillo de realizar, pero que está al alcance de gran número de grupos de investigación en todo el mundo.
En el experimento se han usado tres fuentes de parejas de fotones a 1550 nm entrelazados en polarización (en la figura 
Carlos (amigo de Alicia) y Débora (amiga de Berto) realizan una medida no destructiva de la polarización de los fotones 
Alicia y Berto realizan un medida de observables adecuados sobre dicho estado entrelazado de cuatro fotones, obteniendo los cuatro posibles resultados 
La verificación experimental de un teorema matemático puede parecer irrelevante para un matemático. Pero para el físico sirve como evidencia de que las hipótesis que subyacen a dicho teorema son físicas. Así tenemos evidencia de que los «hechos» (medidas almacenadas en una memoria) son dependientes del observador. Si no lo fueran, o bien se incumplen los axiomas de la mecánica cuántica, o bien el universo es superdeterminista, o bien existe una teoría clásica de variables ocultas no local subyacente que explica la mecánica cuántica. Para un físico en el siglo XXI, la respuesta de consenso es que los «hechos» son dependientes del observador; un filósofo quizás prefiera dedicar una extensa discusión a la falacia de considerar «hechos» los resultados almacenados en la memoria física de un observador, o a la falacia de considerar que un fotón pueda ser un observador, o a cualquier otra cuestión metafísica. Pero un físico del siglo XXI no debería tener dudas sobre estos experimentos de tipo Bell.
Suscribirse a:
Entradas (Atom)
-
... Cuando de repente abres los ojos y te das cuenta que todxs a tu alrededor están muertos...
-
El amor no es tema de conversación hoy en día, en un mundo individualista en el que todo se compra y vende de manera rápida el amor, como t...
-
Los momentos de reflexión últimamente se han tornado continuos formando parte de esa existencia irreal que ha rodeado mi vida. Momentos dis...
-
Película Hierro (3) https://pelis247.org/bin-jip-hierro-3-2004/
-
El pueblo unido jamás será vencido ... de pie marchar el pueblo va a ganar...
