Ilusiones infundadas: Los hechos en mecánica cuántica dependen del observador

La ciencia de la mula Francis

Los «hechos» en mecánica cuántica dependen del observador

El resultado de una medida de un sistema cuántico se puede considerar un «hecho» observado. ¿Son estos «hechos» independientes del observador? No, en mecánica cuántica todo «hecho» depende del observador. Caslav Brukner (Univ. Viena, Austria) demostró un teorema no-go que así lo afirma y propuso un experimento de tipo Bell inspirado en el amigo de Wigner para comprobarlo. Alessandro Fedrizzi (Univ. Heriot-Watt, Edimburgo, Reino Unido) y sus colegas han realizado este experimento con fotones, que toman el papel de los dos superobservadores (los dos Wigner) y de los dos observadores (los dos amigos de Wigner). Así se ha verificado de forma experimental el teorema de Brukner (como no podía ser de otra forma si suponemos que la mecánica cuántica describe nuestro universo). Como hubiera dicho Einstein, si el experimento hubiera contradicho el teorema, no hubiera fallado el teorema, sino el experimento.

Por supuesto, como todos los experimentos de tipo Bell, no está libre de todas las posibles lagunas (o resquicios). La desigualdad CHSH (por Clauser–Horne–Shimony–Holt) afirma que la probabilidad conjunta de los resultados de las cuatro medidas (dos de los observadores y dos de los superobservadores) debe ser menor que 2 (si existe una teoría clásica local subyacente descrita mediante variables ocultas que explica el resultado). Las medidas experimentales (tras estudiar las 64 configuraciones posibles en 1794 repeticiones tras 360 horas de trabajo) ofrecen un valor de 2.416 ± 0.075, una violación de la desigualdad CHSH a más de cinco sigmas (desviaciones estándar). Un resultado rotundo donde los haya (aunque siempre en Física habrá que esperar a que sea repetido de forma independiente). Los «hechos» (resultados de las medidas cuánticas) son dependientes del observador.

El artículo es Massimiliano Proietti, Alexander Pickston, …, Alessandro Fedrizzi, “Experimental rejection of observer-independence in the quantum world,” arXiv:1902.05080 [quant-ph]; el teorema no-go y el experimento mental es publicó en Caslav Brukner, “A no-go theorem for observer-independent facts,” Entropy 20: 350 (2018), doi: 10.3390/e20050350, arXiv:1804.00749 [quant-ph]. En la tertulia del podcast Coffee Break: Señal y Ruido se habló de este tema (LCMF, 01 Mar 2019) al hilo de los «hechos alternativos» en el titular de la pieza de Anil Ananthaswamy, “Quantum experiment suggests there really are ‘alternative facts’,” New Scientist, 22 Feb 2019.

La presentación detallada de un experimento de tipo Bell requiere usar matemáticas. Sin ellas, los razonamientos parecen pura «magia cuántica». Debo empezar recomendando la lectura del libro de John S. Bell, “Lo decible y lo indecible en mecánica cuántica”, Alianza Editorial (1991). Solo tras acostumbrarse a los experimentos de tipo Bell más sencillos se pueden entender los más refinados publicados muchasdécadas más tarde. Como dice la reseña de Carlos Sabín Lestayo, “Confusión cuántica. Tópicos peligrosos en la divulgación de la física cuántica”, Investigación y Ciencia (Feb 2019) [reseña gratuita], mucha gente afirma que no se entiende la mecánica cuántica al hilo de la célebre boutade de Richard Feynman: «Creo que puedo decir con seguridad que nadie entiende la mecánica cuántica». “Las malas citas, sacadas de contexto y sin conocer la fuente original, son una de las plagas de nuestros tiempos. [Siendo] cierto que Feynman pronunció esas palabras, ¿seguro que quería decir lo que parece que quería decir? Si saben inglés, pongan «Richard Feynman, why» en YouTube y prepárense a disfrutar durante siete minutos”.

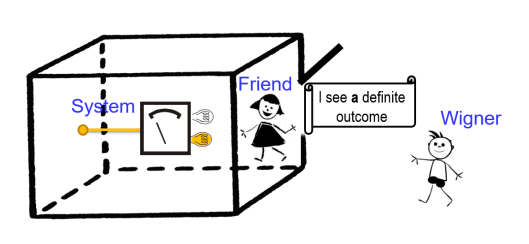
En el experimento del amigo de Wigner intervienen un superobservador(Wigner), capaz de realizar medidas cuánticas sobre sistemas macroscópicos (todo el laboratorio que contiene a su amigo y un cúbit) y un observador (el amigo de Wigner) que solo es capaz de realizar medidas cuánticas sobre sistemas microscópicos. Wigner lo ignora, pero su amigo ha realizado una medida cuántica sobre el cúbit, ha anotado que lo ha hecho en una carta sin indicar el resultado y se la ha enviado por correo a Wigner. Wigner para conocer el estado del cúbit aplica una operación cuántica al laboratorio que borra el estado de la memoria de su amigo y realiza una medida del estado conjunto. Antes de leer la nota, Wigner usa el resultado de su medida para inferir el valor del cúbit. Sin embargo, un día después, tras leer la nota, descubre que su cálculo está mal y que si su amigo ha realizado la medida, su predicción original está en contradicción con lo que ha podido medir el amigo. ¿La mecánica cuántica es incoherente? No, todo lo contrario, tras conocer la nota Wigner debe reevaluar el resultado de su experimento. Si lo hace siguiendo las leyes de la mecánica cuántica, su resultado será compatible con la observación del amigo.

Sean Wigner y su amiga (sigo el dibujo de Brukner); sea el sistema cuántico medido un espín ( $S$ ). La amiga realiza una medida cuántica en la dirección del eje $z$ del espín $S$ que ha sido preparado en el estado $|x+\rangle_S=\frac{1}{\sqrt2}(|z+\rangle_S+|z-\rangle_S)$ . El estado del espín se proyecta y la amiga registra en su memoria el valor obtenido, sea ↑ (hacia arriba) o ↓ (hacia abajo); además, escribe una carta que envía a Wigner por correo. Ignorando lo todo que ha ocurrido en el interior del laboratorio, Wigner asume que ha evolucionado de forma unitaria. Los posibles estados del espín $|z+\rangle_S$ y $|z-\rangle_S$ se suponen que están asociados a los estados de la amiga y de todo el laboratorio, aunque estos sean macroscópicos, resultando dos estados ortogonales $|F_{z+}\rangle_F$ y $|F_{z-}\rangle_F$ . Así el estado del sistema compuesto por el espín, el amigo y el laboratorio es

$|\Phi\rangle_{SF}= \frac{1}{\sqrt2} \left(|z+\rangle_S|F_{z+}\rangle_F+|z-\rangle_S|F_{z-}\rangle_F \right)$ .

Siendo un superobservador, Wigner puede realizar una medida tipo Bell de este sistema macroscópico en la base

$|\Phi^{\pm}\rangle_{SF}=\frac{1}{\sqrt2} \left(|z+\rangle_S|F_{z+}\rangle_F \pm |z-\rangle_S|F_{z-}\rangle_F \right)$ ,

$|\Psi^{\pm}\rangle_{SF}=\frac{1}{\sqrt2} \left(|z+\rangle_S|F_{z-}\rangle_F \pm |z-\rangle_S|F_{z+}\rangle_F \right)$ .

La medida arrojará un resultado que permitirá a Wigner predecir en qué estado está el espín. Pero Wigner no sabe que su amiga le ha enviado una carta; cuando la recibe se da cuenta de que el estado del sistema macroscópico es

$|\Phi\rangle_{SFM}= \frac{1}{\sqrt2} \left(|z+\rangle_S|F_{z+}\rangle_F+|z-\rangle_S|F_{z-}\rangle_F \right) |\textrm{``carta con mensaje: he medido''}\rangle_M$ .

Ahora se da cuenta de que su inferencia anterior del estado del espín a partir del resultado de su medida es incorrecta. Como experto en mecánica cuántica, revisará sus cálculos. Los «hechos» para Wigner (resultados de sus medidas) y los «hechos» para su amiga (resultados de las de ella) han coexistido (hasta que Wigner recibió la carta) como «hechos» dependientes del observador. Solo tras la recepción de la carta y la reevaluación del significado de los resultados sobre el estado del espín estos «hechos» se consensúan y adquieren la propiedad de ser «hechos» sobre el espín independientes del observador.

Este experimento se puede complicar si contamos con dos Wigner (superobservadores) y dos amigos de Wigner (observadores). Y más aún, si tenemos en cuenta el orden temporal en el que se realizan las medidas cuánticas. Así llegamos a un experimento engorroso de analizar en el que es muy fácil perder el hilo y acabar realizando operaciones matemáticas en contra de los postulados de la mecánica cuántica. Por ejemplo, suponer que la evolución es unitaria tras una medida, como si no hubiera ocurrido una proyección del estado (el mal llamado colapso). Ya te puse un buen ejemplo en “El error del artículo de Frauchiger y Renner sobre la inconsistencia de la mecánica cuántica”, LCMF, 29 Oct 2018; en rigor tendría que haber titulado «incoherencia», evitando el anglicismo «inconsistencia», un falso amigo bien conocido). Si todas las medidas son unitarias (ninguna tiene proyección el estado), o si todas las medidas incluyen una proyección del estado (ninguna es unitaria), el resultado siempre está de acuerdo con la mecánica cuántica y no hay ningún tipo de incoherencia. Pero si seguimos los cálculos realizados por Frauchiger y Renner al pie de la letra, con medidas que a veces proyectan el estado y que otras veces no lo proyectan, aparece una incoherencia. Pero su origen no es la incoherencia de la mecánica cuántica, como ellos afirman y los medios cacarean, sino la incoherencia del análisis realizado por Frauchiger y Renner.

El teorema no-go de Brukner afirma que no existen hechos independientes del observador. En concreto, se demuestra que las cuatro afirmaciones siguientes son contradictorias: (1) la teoría cuántica es válida (en nuestro universo y a todas las escalas); (2) las medidas cuánticas de los observadores son locales (no se propaga información entre observadores más rápido que la velocidad de la luz en el vacío); (3) el universo no es superdeterminista (los observadores tienen libre albedrío a la hora de preparar el estado de sus sistemas de medida); y (4) los «hechos» (resultados de las medidas registrados en memorias físicas) son independientes del observador. Como todo físico que acepta la mecánica cuántica considera que las tres primeras afirmaciones son incuestionables, la conclusión es que todos los «hechos» son dependientes del observador.

Para confirmar su teorema de forma experimental, Brukner nos propone el experimento ilustrado en esta figura, con dos Wigner (superobservadores) llamados Alicia y Berto, y dos amigos (observadores) llamados Carlos y Débora. Entre los dos laboratorios hay generador de una pareja de espines entrelazados que se envían hacia Carlos, sea $S_1$ , y hacia Débora, sea $S_2$ . El estado inicial de la pareja de espines es

$|\psi\rangle_{S_1S_2}=-\sin\frac{\theta}{2} |\phi^+\rangle_{S_1S_2}+\cos\frac{\theta}{2} |\psi^-\rangle_{S_1S_2}$ ,

donde

$|\phi^+\rangle_{S_1S_2} = \frac{1}{\sqrt{2}} (|z+\rangle_{S_1}|z+\rangle_{S_2} + |z-\rangle_{S_1}|z-\rangle_{S_2})$ ,

$|\psi^-\rangle_{S_1S_2} = \frac{1}{\sqrt{2}} (|z+\rangle_{S_1}|z-\rangle_{S_2} - |z-\rangle_{S_1}|z+\rangle_{S_2})$ .

En ángulo $\theta$ , con el que Débora ha rotado en el eje $y$ el espín, se introduce como parámetro libre cuyo valor óptimo maximizará el incumplimiento de la desigualdad de tipo Bell. Para los superobservadores, Alicia y Berto, el estado de los espines que se encuentran dentro de los laboratorios de Carlos y Débora se describe por

$|\Psi_0\rangle= |\psi\rangle_{S_1S_2} |0\rangle_C |0\rangle_D$ ,

Carlos y Débora realizarán una medida de sus respectivos espines a lo largo del eje $z$ ; aunque proyectan el estado de dicho espín, a los ojos ignorantes de Alicia y Berto los espines han evolucionado de forma unitaria, sin proyección del estado. Por tanto, para ellos

$|\tilde{\Psi}\rangle =-\sin\frac{\theta}{2} |\Phi^+\rangle + \cos\frac{\theta}{2} |\Psi^-\rangle$ ,

donde

$|\Phi^+\rangle = \frac{1}{\sqrt{2}} (|A_{up}|B_{up}\rangle + |A_{down}\rangle|B_{down}\rangle)$ ,

$|\Psi^-\rangle = \frac{1}{\sqrt{2}} (|A_{up}\rangle |B_{down}\rangle - |A_{down}\rangle |B_{up}\rangle )$ ,

$|A_{up}\rangle=|z+\rangle_{S_1}|C_{z+}\rangle_{C},\qquad |B_{up}\rangle=|z+\rangle_{S_2}|D_{z+}\rangle_{D}$ ,

$|A_{down}\rangle=|z-\rangle_{S_1}|C_{z-}\rangle_{C}, \qquad |B_{down}\rangle =|z-\rangle_{S_2}|D_{z-}\rangle_{D}$ .

Se definen los resultados observados para los espines en los ejes $z$ y $x$ para Alicia como

$A_z=|A_{up}\rangle\langle A_{up}|-|A_{down}\rangle\langle A_{down}|$ ,

$A_x=|A_{up}\rangle\langle A_{down}|+|A_{down}\rangle\langle A_{up}|$ ,

y los análogos $B_z$ y $B_x$ para Berto. En este experimento de tipo Bell habrá dos elecciones (haciendo uso de su «libre albedrío»), la de Alicia entre $A_1=A_z$ y $A_2=A_x$ , y la de Berto entre $B_1=B_z$ y $B_2=B_x$ ; en un experimento tipo amigo de Wigner estas elecciones corresponden a elegir entre los resultados de los amigos ( $A_1$ y $B_1$ ) y de los Wigner ( $A_2$ y $B_2$ ).

La desigualdad de tipo Bell para este experimento será de tipo Clauser-Horne-Shimony-Holt (CHSH). Por tanto, relacionará la probabilidad conjunta $p(A_1,A_2,B_1,B_2)$ con las probabilidades marginales

$p(A_1,B_1) =\sum_{A_2,B_2=-1,1} p(A_1,A_2,B_1,B_2)$ ,

$\langle A_1 B_1 \rangle = \sum_{A_1,B_1=-1,1} A_1 B_1 p(A_1, B_1)$ ,

y de forma similar en los otros casos, donde se han tomado valores numéricos para $A_1$ , $A_2$ , $B_1$ , y $B_2$ en $\{+1,-1\}$ . Asumiendo la existencia de una teoría clásica de variables ocultas subyacente, es decir, que las probabilidades están regidas por una teoría clásica de la probabilidad, un cálculo engorroso, pero estándar, permite obtener la desigualdad CHSH dada por

$S = \langle A_1B_1 \rangle + \langle A_1B_2 \rangle+\langle A_2B_1 \rangle-\langle A_2B_2 \rangle\leq 2$ .

El cálculo cuántico, es decir, que usa amplitudes de probabilidad en lugar de probabilidades, conduce a una cota superior diferente $S_Q(\theta)$ . Se valor máximo, para $\theta=\pi/4$ , está dado por $S_Q= 2\sqrt{2}$ . Nótese lo obvio, que la mecánica cuántica incumple la desigualdad CHSH, dado que $2\sqrt{2} > 2$ .

Esta figura muestra el esquema experimental de la implementación óptica de Proietti y sus colegas del experimento mental de Brukner. En lugar de humanos se usan fotones como observadores y superobservadores, y también en lugar de los dos espines. En rigor la mecánica cuántica permite que el observador sea una sistema cuántico; lo único que caracteriza al observador es disponer de una memoria en la que se almacene el resultado de la medida (es decir, la capacidad de generar un «hecho»; los filósofos que lean esto sabrán que hay otras definiciones del término «hecho», pero nos alejaría de nuestro objetivo discutirlas). Gracias a ello se puede implementar un superobservador capaz de observar un observador, es decir, un sistema cuántico capaz de medir a un sistema cuántico capaz de medir a un sistema cuántico. En algunos foros de la web se ha criticado que en este experimento todos los sistemas cuánticos sean fotones; se sugiere que una implementación más rigurosa exige que el sistema observado, los observadores y los superobservadores sean sistemas físicos diferentes. En rigor es innecesario, lo que no quitará que un futuro muy cercano se logre dicha implementación. Usando solo fotones todas las operaciones cuánticas se realizan con tecnología fotónica en una mesa óptica, lo que facilita la implementación del experimento, que no es sencillo de realizar, pero que está al alcance de gran número de grupos de investigación en todo el mundo.

En el experimento se han usado tres fuentes de parejas de fotones a 1550 nm entrelazados en polarización (en la figura $S_0$ , $S_A$ y $S_B$ ). Usando tomografía del estado cuántico se ha comprobado su alta fiabilidad, $\mathcal{F}=99.62^{+0.01}_{-0.04}\%$ , alta pureza, $\mathcal{P}=99.34^{+0.01}_{-0.09}\%$ , y buen entrelazamiento, medido con su concurrencia, $\mathcal{C}=99.38^{+0.02}_{-0.10}\%$ . El par de fotones de la fuente $S_0$ se denominan $a$ y $b$ , este último rotado un ángulo adecuado para maximizar el incumplimiento de la desigualdad CHSH.

Carlos (amigo de Alicia) y Débora (amiga de Berto) realizan una medida no destructiva de la polarización de los fotones $a$ y $b$ , resp., que reciben desde $S_0$ . La información de la medida se almacena en el estado de polarización de los fotones $\alpha$ y $\beta$ que reciben de las fuentes $S_A$ y $S_B$ , resp., que actúan como sus memorias de observadores. Los otros fotones de estas fuentes, $\alpha'$ y $\beta'$ son absorbidos (descartados sin que ninguna medida desvele su estado); este descarte se retrasa un tiempo suficiente como para que se realice cuando todo lo demás haya finalizado y no afecte a los demás resultados (salvo que se incumpla la hipótesis de causalidad). Según la perspectiva de Alicia y Berto, los fotones aún no observados de las fuentes $S_0$ , $S_A$ y $S_B$ se encuentran en un estado entrelazado de cuatro fotones. Los detalles matemáticos se encuentran en la información suplementaria del artículo, que recomiendo consultar a los interesados.

Alicia y Berto realizan un medida de observables adecuados sobre dicho estado entrelazado de cuatro fotones, obteniendo los cuatro posibles resultados $A_0$ , $B_0$ , $A_1$ , y $B_1$ . El experimento consiste en repetir el experimento muchas veces para estimar la probabilidad conjunta $P(A_0,A_1,B_0,B_1)$ , que cumplirá la desigualdad CHSH (si el cálculo se realiza con probabilidades clásicas). Esta figura muestra los resultados obtenidos para las estimaciones de las probabilidades marginales (puntos azules), comparándolas con las predicciones teóricas (barras naranjas). El resultado obtenido $S_{\textrm{exp}} = 2.416^{+0.075}_{-0.075}$ , incumple con la desigualdad CHSH con más de cinco desviaciones estándares.

La verificación experimental de un teorema matemático puede parecer irrelevante para un matemático. Pero para el físico sirve como evidencia de que las hipótesis que subyacen a dicho teorema son físicas. Así tenemos evidencia de que los «hechos» (medidas almacenadas en una memoria) son dependientes del observador. Si no lo fueran, o bien se incumplen los axiomas de la mecánica cuántica, o bien el universo es superdeterminista, o bien existe una teoría clásica de variables ocultas no local subyacente que explica la mecánica cuántica. Para un físico en el siglo XXI, la respuesta de consenso es que los «hechos» son dependientes del observador; un filósofo quizás prefiera dedicar una extensa discusión a la falacia de considerar «hechos» los resultados almacenados en la memoria física de un observador, o a la falacia de considerar que un fotón pueda ser un observador, o a cualquier otra cuestión metafísica. Pero un físico del siglo XXI no debería tener dudas sobre estos experimentos de tipo Bell.

martes, 5 de marzo de 2019

Los hechos en mecánica cuántica dependen del observador

No hay comentarios:

Publicar un comentario

Micropensamiento. Las mentiras y yo